Let’s examine the Squeeze Theorem, or the Sandwich Theorem, which lets us determine a function’s limit at x = a when that function is squeezed between two other functions that have equal limits at that x-value. Let’s look at some examples to see how to use it, and an interactive Desmos calculator to visualize what’s going on.

The “Squeeze” or “Sandwich” names are apt, because the theorem says that if your function always lies between two other functions near the point of interest, and those functions have equal limits there, then your function must have the same limit because it’s “squeezed” between the other two.

The Squeeze (or Sandwich) Theorem
If $g(x) \le f(x) \le h(x)$ when x is near a, except perhaps at a, and
\[\lim_g(x) = \lim_h(x) = L\] then
\[\lim_f(x) = L\]

The following example illustrates. We’re going to revisit a limit we looked at earlier, when we used Desmos graphs to examine “Some Limits That Do Exist; Some That Do Not”: $\displaystyle< \lim_x \cos\left(\dfrac \right)>.$ You might recall the discussion there between Luis and Qiao about whether the limit exists and equals 0, or does not exist at all because $\cos(1/x)$ oscillates wildly near $x=0.$. Let’s now reason about the limit without relying on Desmos.

Prove $\displaystyle< \lim_x \cos(1/x)= 0>.$

Solution.
This is a classic use of the Squeeze theorem involving an oscillating trig function, either sine or cosine. You should always start your proof with the trig function itself, using the fact that no matter what the argument is, sin and cosine simply oscillate between $-1$ and 1, and never exceed those bounds. Here, then, our first line is
\[-1 \le \cos(1/x) \le 1 \] Next, recall that the function we’re interested in is $x \cos(1/x).$ So we multiply each term in the line above by x to force our function to be in the middle:
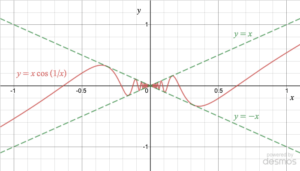
\[-x \le x\cos(1/x) \le x\] So our function of interest is always squeezed between $-x$ and $x.$ (You can see this in an interactive graph below.)

Now, since we know
\[\lim_(-x) = 0 \quad \text \quad \lim_x =0 \] we immediately conclude by the Squeeze Theorem
\[\lim_x\cos(1/x) = 0 \quad \cmark\] That’s it: your proof ends there.

To understand what’s going on visually, the interactive Desmos calculator shows the function $f(x) = x\cos(1/x)$ as a solid red curve, while the green dashed lines indicate $y=x$ and $y=-x.$ You can see how near $x=0$ the x acts as an “envelope” for the cosine function, bounding (or “squeezing”) its amplitude. Said differently, the amplitude of this oscillating function is always x, so since $\displaystyle<\lim_(\pm x) =0>,$ the function is forced to 0 as $x \to 0.$ Using the buttons beneath the graph, you can view the original function $f(x),$ or just $\cos(1/x),$ or just the lines $y = \pm x.$

Note in particular how $\displaystyle<\lim_\cos(1/x)>$ does not exist, but the “squeezed” function $f(x) = x\cos(1/x)$ is forced to 0 as $x \to 0.$ That’s the Squeeze theorem at work!

There is one other typical problem-type that requires use of the Squeeze Theorem, as illustrated in Example 2. In this type, you don’t know anything about the function of interest other than that it always lies between two other (known) functions – and that’s enough to be able to use the Squeeze Theorem.

If
\[3x – 4 \le f(x) \le x^2 -3x +5 \text < for >x \ge 0,\] find $\displaystyle<\lim_f(x)>.$

Solution.
In a problem like this, it will always be the case that the two functions that squeeze the function of interest, $f(x),$ have equal limits at the x-value of interest. Here, for instance, we have
\[\lim_(3x – 4) = 5 \quad \text \quad \lim_\left( x^2 -3x +5\right) = 5\] Hence since $3x – 4 \le f(x) \le x^2 -3x +5,$ and we just determined the limits of the two bounding functions at $x = 3,$ we conclude using the Squeeze Theorem that
\[\lim_f(x) = 5 \quad \cmark \]

Because it’s of such limited use, problems requiring the Squeeze Theorem don’t appear frequently on exams and sometimes isn’t even required for any homework problems. Please check with your instructor whether you need to know how to use it to find a limit. That said, we will need it later to prove an important theorem, so keep it in the back of your mind!

The Upshot

1. The Squeeze, or Sandwich, Theorem says that if a function f lies between two other functions near the point of interest, and those functions have the same limit L at that point, then f has that limit there as well.

On the next screen, we’ll look at a few limits involving trig functions that, early in your Calculus studies, you simply have to memorize. Although this has been a brief discussion, if you have questions or comments about the Squeeze Theorem we’d love to hear them over on the Forum!

If we've helped you learn something,
perhaps you'd like to give back a little something and

☕ Buy us a coffee We're working to add more,
and would appreciate your help
to keep going! 😊